Segment

Contains geometric measurements based on a polygonal approximation of the 2D object boundaries.

More information about the segment objects is available in the polygonal approximation section.

Note: These measurements ignore the intensity input image.

Object members

Measurement name	Description	Element type	Indexing
PolygoneArea2d	The area computed from the vectorized edges of the object, expressed in the image calibration unit. The vectorized edges are extracted by polygonal approximation.	Floating point	[label]
PolygonePerimeter2d	The perimeter computed as the vectorized edges length of the object, expressed in the image calibration unit. The vectorized edges are extracted by polygonal approximation.	Floating point	[label]
ConvexArea2d	The area of the vectorized edges convex hull of the object, expressed in the image calibration unit. The vectorized edges are extracted by polygonal approximation.	Floating point	[label]
ConvexPerimeter2d	The perimeter of the vectorized edges convex hull of the object, expressed in the image calibration unit. The vectorized edges are extracted by polygonal approximation.	Floating point	[label]
SmoothCircleDifference2d	The difference between the object area and the area of its smoothing circle, expressed in the image calibration unit. The Smooth Circle Difference Area $SCDA$ is given from the object area $A$ and the area of its smoothing circle $SCA$ by: $$ SCDA = \cup(A,SCA) - \cap(A,SCA)$$ The smoothing circle is computed on the polygonal approximation of the object boundary and verifies: The center of the circle is the barycenter of the object. The distance between the circle and the approximated polygon minimizes the least squares criteria.	Floating point	[label]
EnclosingCircleDifference2d	The difference between the object area and the area of its enclosing circle, expressed in the image calibration unit. The Enclosing Circle Difference Area $ECDA$ is given from the object area $A$ and the area of its enclosing circle $ECA$ by: $$ ECDA = \cup(A,ECA) - \cap(A,ECA)$$ The enclosing ellipse is computed on the polygonal approximation of the object boundary and verifies: The center of the ellipse is the barycenter of the object. The circle diameter is given by the extent size of the largest eigenvector of the covariance matrix.	Floating point	[label]
EnclosingEllipseDifference2d	The difference between the object area and the area of its enclosing ellipse, expressed in the image calibration unit. The Ellipse Difference Area $EEDA$ is given from the object area $A$ and the area of its enclosing ellipse $EEA$ by: $$ EEDA = \cup(A,EEA) - \cap(A,EEA)$$ The enclosing ellipse is computed on the polygonal approximation of the object boundary and verifies: The center of the ellipse is the barycenter of the object. The major axis of the ellipse is parallel to the inertia axis of the object. The length of the minor and major axis is given by the extent size of the eigenvectors of the covariance matrix.	Floating point	[label]
RectangleCenterX2d	The X coordinate of the Rectangle of Minimum Area center, expressed in the coordinate system defined by the image calibration. The Rectangle of Minimum Area is the rectangle of minimum area enclosing the object polygonal approximation.	Floating point	[label]
RectangleCenterY2d	The Y coordinate of the Rectangle of Minimum Area center, expressed in the coordinate system defined by the image calibration. The Rectangle of Minimum Area is the rectangle of minimum area enclosing the object polygonal approximation.	Floating point	[label]
RectangleLength2d	The length of the Rectangle of Minimum Area, expressed in the image calibration unit. The Rectangle of Minimum Area is the rectangle of minimum area enclosing the object polygonal approximation.	Floating point	[label]
RectangleWidth2d	The width of the Rectangle of Minimum Area, expressed in the image calibration unit. The Rectangle of Minimum Area is the rectangle of minimum area enclosing the object polygonal approximation.	Floating point	[label]
RectangleOrientation2d	The orientation angle of the Rectangle of Minimum Area, in degrees, in the range [0,180]. The Rectangle of Minimum Area is the rectangle of minimum area enclosing the object polygonal approximation.	Floating point	[label]
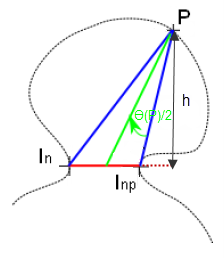
Rugosity2d	The factor of rugosity determines if the contour of a shape is smooth or not. Its value is close to 1 for an abrasive shape and decreases for smooth boundaries. Rugosity, also known as 'spike parameter', is given by the formula $Ru(P)=E_{D}(Ru_{d}(P))$ where $E_{D}$ is the mean operator over all the triangle basis $d\in \lbrack 40,L/15 \lbrack$. The step length $d$ represents the distance $\overline{I_{n}I_{np}}$ in figure 1. $L$ is defined as the shape perimeter in pixels. $Ru_{d}(P)$ is defined as follows: $$ Ru_{d}(P) = E_N(ru_{n})$$ where: $E_N$ is the mean operator over all the valid $[In,Inp]$ bases for the current $d$ length $ru_{n} = cos(\theta(n)/2)\times \theta(n)$ $\theta(n)$ is the angle associated with the point $P$ maximizing the spike value $cos(\theta(P)/2)\times h$ The angle $\theta$ and the distance $h$ are defined as in the figure below $\theta < 2.9 \mbox{ rad}$, if $\theta \geq 2.9 \mbox{ rad}$ the spike value is counted as 0 Fig 1. Determination of the spike value related to a given base For more information: M.G. Hamblin, G.W. Stachowiak, "A multi-scale measure of particle abrasivity", Wear vol. 185, pp. 225-233, Jun. 1995.	Floating point	[label]
BorderDistance2d	The shortest edge-to-edge distance from the current object to its nearest neighbor, expressed in the image calibration unit. This distance measurement is computed on the polygonal approximation of the object boundaries.	Floating point	[label]
PolygoneHoleCount2d	The number of holes of the particles represented by the inner and outer chains. This number is computed on the polygonal approximation of the object boundaries.	Integer	[label]
InsideLength2d	The length of the object skeleton, expressed in the image calibration unit. This measurement represents the geodesic distance between the two furthest points of the object boundary polygonal approximation.	Floating point	[label]
InsideCenterX2d	The X coordinate of the inside length center, expressed in the coordinate system defined by the image calibration. Unlike the barycenter, this measurement ensures to return a point belonging to the object. This measurement is extracted from the skeleton of the object boundary polygonal approximation.	Floating point	[label]
InsideCenterY2d	The Y coordinate of the inside length center, expressed in the coordinate system defined by the image calibration. Unlike the barycenter, this measurement ensures to return a point belonging to the object. This measurement is extracted from the skeleton of the object boundary polygonal approximation.	Floating point	[label]