Opening And Closing
Morphological opening and closing algorithms.
- Opening2d: Performs a two-dimensional opening using a structuring element matching with a square or a cross.
- Opening3d: Performs a three-dimensional opening using a structuring element matching with a with a full or partial cube.
- Closing2d: Performs a two-dimensional closing using a structuring element matching with a square or a cross.
- Closing3d: Performs a three-dimensional opening using a structuring element matching with a with a full or partial cube.
- OpeningDisk2d: Performs a two-dimensional opening using a structuring element matching with a disk.
- OpeningDisk3d: Performs a three-dimensional opening using a structuring element matching with an oriented disk.
- OpeningBall3d: Performs a three-dimensional opening using a structuring element matching with a sphere.
- ClosingDisk2d: Performs a two-dimensional closing using a structuring element matching with a disk.
- ClosingDisk3d: Performs a three-dimensional closing using a structuring element matching with an oriented disk.
- ClosingBall3d: Performs a three-dimensional closing using a structuring element matching with a sphere.
- OpeningLine2d: Performs a two-dimensional opening using a structuring element matching with a line.
- OpeningLine3d: Performs a three-dimensional opening using a structuring element matching with a line.
- ClosingLine2d: Performs a two-dimensional closing using a structuring element matching with a line.
- ClosingLine3d: Performs a three-dimensional closing using a structuring element matching with a line.
- OpeningLineMaximum: Performs a maximal linear opening.
- ClosingLineMinimum: Performs a minimal linear closing.
- OpeningColor2d: Performs an opening on a true-color image using a structuring element matching with a square.
- ClosingColor2d: Performs a closing on a true-color image using a structuring element matching with a square.
- OpeningByReconstruction2d: Performs a two-dimensional opening by reconstruction with a structuring element matching with a square.
- OpeningByReconstruction3d: Performs a three-dimensional opening by reconstruction with a structuring element matching with a cube.
- ClosingByReconstruction2d: Performs a two-dimensional closing by reconstruction with a structuring element matching with a square.
- ClosingByReconstruction3d: Performs a three-dimensional closing by reconstruction with a structuring element matching with a cube.
- OpeningDiskByReconstruction2d: Performs a two-dimensional opening by reconstruction with a structuring element matching with a disk.
- OpeningBallByReconstruction3d: Performs a three-dimensional opening by reconstruction with a structuring element matching with a sphere.
- ClosingDiskByReconstruction2d: Performs a three-dimensional closing by reconstruction with a structuring element matching with a disk.
- ClosingBallByReconstruction3d: Performs a three-dimensional closing by reconstruction with a structuring element matching with a cube.
- SelectiveOpening2d: Opens objects of a two-dimensional binary image conditionally to a local constraint.
- SelectiveOpening3d: Opens objects of a three-dimensional binary image conditionally to a local constraint.
- SelectiveClosing2d: Closes objects of a two-dimensional binary image conditionally to a local constraint.
- SelectiveClosing3d: Closes objects of a three-dimensional binary image conditionally to a local constraint.
For an introduction:
The opening by a disk, $B$, is the combination of an erosion $E$ followed by a dilation $D$, using the $B$ structuring element for both operations.
The opened image $I$ is denoted $O_B(I)$ or $O(I)$ and is defined as: $O_B(I)=D_B(E_B(I))$.
Considering a disk as structuring element, as shown in Figure 1, the opening is achieved by sliding the disk inside the object and discarding all the parts where the disk cannot fit.
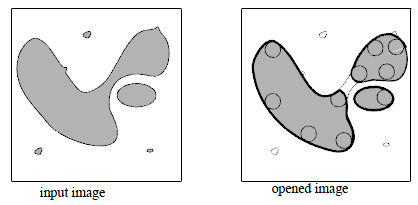
Figure 1. Effect of an opening
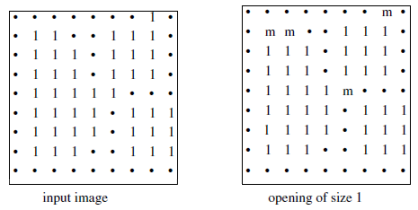
Figure 2. An opening of size 1
In this case, when the rectangle is totally included in the set $X$, all the points of the rectangle are kept; in the case of the erosion, only the central pixel was kept.
One may also notice that the largest particle has been split in two parts, and that it has lost its two small peaks. The other particle has not been modified.
A closing by a disk $B$ is a dilation $D$ followed by an erosion $E$, using the $B$ structuring element for both operations.
The closing of the image $I$ will be denoted $C_B(I)$ or $C(I)$ and is defined as: $C_B(I) = E_B(D_B(I))$.
A closing fills the holes inside the particles, eliminates the small details by smoothing the boundary from the outside, and connects close particles.
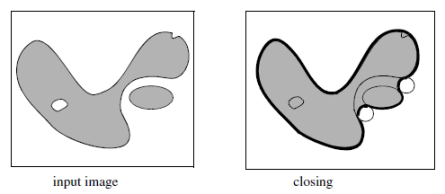
Figure 3. Effect of a closing
As shown in Figure 3, the closing is achieved by sliding the disk outside the particle and filling all the parts the disk cannot fit into. Figure 4 represents the same original image as in Figure 3 and a closing by an hexagon of size 1.
The closing smooths the largest particle and connects the two particles of the image. The two 1 s in the upper right corner appear because the points on the edge of the image cannot be the centre of a complete hexagon. This is called a border effect.
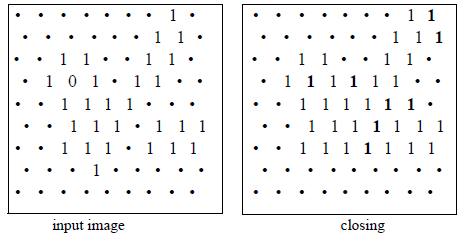
Figure 4. A closing of size 1 applied on an hexagonal grid
- section Mathematical Morphology
- section Erosion And Dilation
Introduction to Opening
An opening does not destroy as much information as an erosion. An opening discards small objects, but retains the larger ones with a shape very similar to that of the original image.The opening by a disk, $B$, is the combination of an erosion $E$ followed by a dilation $D$, using the $B$ structuring element for both operations.
The opened image $I$ is denoted $O_B(I)$ or $O(I)$ and is defined as: $O_B(I)=D_B(E_B(I))$.
Considering a disk as structuring element, as shown in Figure 1, the opening is achieved by sliding the disk inside the object and discarding all the parts where the disk cannot fit.

Figure 1. Effect of an opening
Example
Figure 2 contains the original image of Figure 1 and the result of an opening by a rectangle of size 1. The same structuring element that was used for the erosion has been chosen to compare the two transforms.
Figure 2. An opening of size 1
In this case, when the rectangle is totally included in the set $X$, all the points of the rectangle are kept; in the case of the erosion, only the central pixel was kept.
One may also notice that the largest particle has been split in two parts, and that it has lost its two small peaks. The other particle has not been modified.
Introduction to Closing
A closing is similar to a dilation but also less destructive. Small objects may be joined to larger ones.A closing by a disk $B$ is a dilation $D$ followed by an erosion $E$, using the $B$ structuring element for both operations.
The closing of the image $I$ will be denoted $C_B(I)$ or $C(I)$ and is defined as: $C_B(I) = E_B(D_B(I))$.
A closing fills the holes inside the particles, eliminates the small details by smoothing the boundary from the outside, and connects close particles.

Figure 3. Effect of a closing
Example
As shown in Figure 3, the closing is achieved by sliding the disk outside the particle and filling all the parts the disk cannot fit into. Figure 4 represents the same original image as in Figure 3 and a closing by an hexagon of size 1.
The closing smooths the largest particle and connects the two particles of the image. The two 1 s in the upper right corner appear because the points on the edge of the image cannot be the centre of a complete hexagon. This is called a border effect.

Figure 4. A closing of size 1 applied on an hexagonal grid
© 2025 Thermo Fisher Scientific Inc. All rights reserved.