Rotate2d
Applies a rotation of a given angle on a two-dimensional image around a given point or the center of the image.
Access to parameter description
For an introduction: section 2D Rotations.
This algorithm performs a rotation of an image by a user-defined angle $\theta$ and a center $C$.
The new coordinates $(x', y')$ can be expressed as a function of the old coordinates $(x, y)$: $$ \left\{\begin{matrix}x'&=&(x-x_0)\cdot\cos\theta - (y-y_0)\cdot\sin\theta + x_0\\ y'&=&(x-x_0)\cdot\sin\theta + (y-y_0)\cdot\cos\theta + y_0\end{matrix}\right\} $$ where $(x_0,y_0)$ are the coordinates of the center of the rotation. Or in matrix notation: $$ \begin{bmatrix}x'\\y'\end{bmatrix} = \begin{bmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{bmatrix} \cdot\begin{bmatrix}x-x_0\\y-y_0\end{bmatrix} + \begin{bmatrix}x_0\\y_0\end{bmatrix} $$ If the dimensions of the output image are the same as those of the input, the destination pixels may be outside the image, and these pixels are then ignored. An output resizing option automatically modifies the dimensions of the image to make all the input data visible in the output image. This option is enabled by default.
On the other hand, some pixels in the output image may not have a corresponding pixel in the input image. In this case, a user-defined padding value is assigned to these pixels.
Furthermore, the $(x, y)$ coordinates obtained are not always integers, even though an image is a discrete space. The following figure illustrates the grid of the resultant image, the point $M'$ being a pixel in this image. The points are generated from the rotation of the original image and do not fit on the grid.
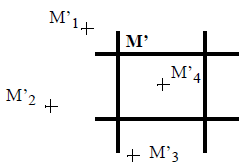
Figure 1. Image grid rotation
To calculate the intensity of each pixel $M'$, two methods are possible:
If $d_j$ denotes the distance $M'_j M'$, $f_i$ is defined as: $$ f_i=\prod_{\substack{j=1\\j\neq i}}^{j=4}d_j $$ e.g., $f_1=d_2d_3d_4$.
The choice of the $f_i$'s ensures that the interpolated value is equal to $g'_j$ if $M'$ matches $M'_j$. This method gives better results but requires more computation time.
Figure 1. Centered 30 degrees rotation of a 1024x1024 image: (a) the input image,
(b) rotation without output resizing (1024x1024 image), (c) rotation with output resizing (1398x1398 image).
See also
Access to parameter description
For an introduction: section 2D Rotations.
This algorithm performs a rotation of an image by a user-defined angle $\theta$ and a center $C$.
The new coordinates $(x', y')$ can be expressed as a function of the old coordinates $(x, y)$: $$ \left\{\begin{matrix}x'&=&(x-x_0)\cdot\cos\theta - (y-y_0)\cdot\sin\theta + x_0\\ y'&=&(x-x_0)\cdot\sin\theta + (y-y_0)\cdot\cos\theta + y_0\end{matrix}\right\} $$ where $(x_0,y_0)$ are the coordinates of the center of the rotation. Or in matrix notation: $$ \begin{bmatrix}x'\\y'\end{bmatrix} = \begin{bmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{bmatrix} \cdot\begin{bmatrix}x-x_0\\y-y_0\end{bmatrix} + \begin{bmatrix}x_0\\y_0\end{bmatrix} $$ If the dimensions of the output image are the same as those of the input, the destination pixels may be outside the image, and these pixels are then ignored. An output resizing option automatically modifies the dimensions of the image to make all the input data visible in the output image. This option is enabled by default.
On the other hand, some pixels in the output image may not have a corresponding pixel in the input image. In this case, a user-defined padding value is assigned to these pixels.
Furthermore, the $(x, y)$ coordinates obtained are not always integers, even though an image is a discrete space. The following figure illustrates the grid of the resultant image, the point $M'$ being a pixel in this image. The points are generated from the rotation of the original image and do not fit on the grid.
Figure 1. Image grid rotation
To calculate the intensity of each pixel $M'$, two methods are possible:
- Take the gray level of the nearest neighbor. For the above example $M'$ would be given the intensity of $M'_1: g'=g'_1$
- Take into account the four nearest neighbors and calculate the gray level based on the average of the four points, weighted by their distance, as in: $$ g'=\frac{f_1\times g'_1+f_2\times g'_2+f_3\times g'_3+f_4\times g'_4}{f_1+f_2+f_3+f_4} $$
If $d_j$ denotes the distance $M'_j M'$, $f_i$ is defined as: $$ f_i=\prod_{\substack{j=1\\j\neq i}}^{j=4}d_j $$ e.g., $f_1=d_2d_3d_4$.
The choice of the $f_i$'s ensures that the interpolated value is equal to $g'_j$ if $M'$ matches $M'_j$. This method gives better results but requires more computation time.
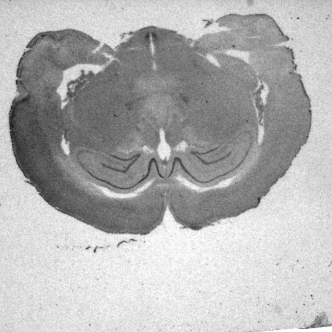 (a) |
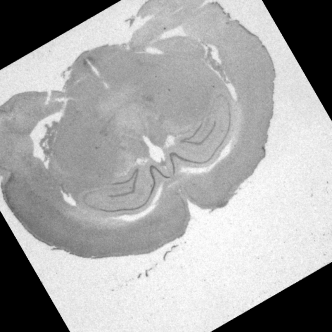 (b) |
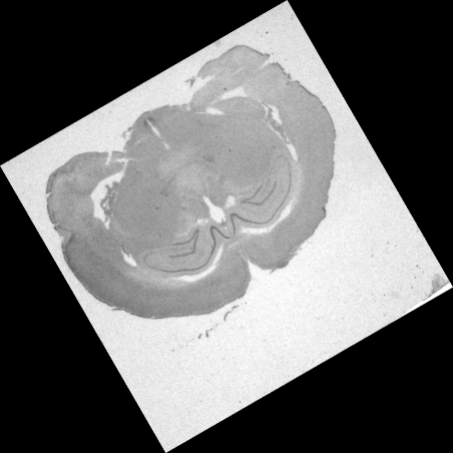 (c) |
(b) rotation without output resizing (1024x1024 image), (c) rotation with output resizing (1398x1398 image).
See also
Function Syntax
This function returns outputImage.
// Function prototype
std::shared_ptr< iolink::ImageView > rotate2d( std::shared_ptr< iolink::ImageView > inputImage, double rotationAngle, Rotate2d::CenterMode centerMode, iolink::Vector2d rotationCenter, Rotate2d::InterpolationType interpolationType, bool outputResizing, double paddingValue, std::shared_ptr< iolink::ImageView > outputImage = nullptr );
This function returns outputImage.
// Function prototype.
rotate_2d(input_image: idt.ImageType,
rotation_angle: float = 90,
center_mode: Rotate2d.CenterMode = Rotate2d.CenterMode.IMAGE_CENTER,
rotation_center: Union[Iterable[int], Iterable[float]] = [0, 0],
interpolation_type: Rotate2d.InterpolationType = Rotate2d.InterpolationType.NEAREST_NEIGHBOR,
output_resizing: bool = True,
padding_value: float = 0,
output_image: idt.ImageType = None) -> idt.ImageType
This function returns outputImage.
// Function prototype.
public static IOLink.ImageView
Rotate2d( IOLink.ImageView inputImage,
double rotationAngle = 90,
Rotate2d.CenterMode centerMode = ImageDev.Rotate2d.CenterMode.IMAGE_CENTER,
double[] rotationCenter = null,
Rotate2d.InterpolationType interpolationType = ImageDev.Rotate2d.InterpolationType.NEAREST_NEIGHBOR,
bool outputResizing = true,
double paddingValue = 0,
IOLink.ImageView outputImage = null );
Class Syntax
Parameters
| Parameter Name | Description | Type | Supported Values | Default Value | |||||
|---|---|---|---|---|---|---|---|---|---|
 |
inputImage |
The input image. | Image | Binary, Label, Grayscale or Multispectral | nullptr | ||||
|
rotationAngle |
The angle of the rotation in degrees. | Float64 | Any value | 90 | ||||
|
centerMode |
The way to define the rotation center
|
Enumeration | IMAGE_CENTER | |||||
|
rotationCenter |
The rotation center coordinates. This parameter is ignored in IMAGE_CENTER mode. | Vector2d | Any value | {0.f, 0.f} | ||||
|
interpolationType |
The interpolation mode. Method used to calculate the intensity of each pixel in the result image.
|
Enumeration | NEAREST_NEIGHBOR | |||||
|
outputResizing |
Resize the output image to make all input data visible in the output image if set to True. Preserve the input dimension if set to False. | Bool | true | |||||
|
paddingValue |
The background value for pixels with no correpondant point in the input image. | Float64 | Any value | 0 | ||||
 |
outputImage |
The output image. Its type is forced to the same values as the input. Its dimensions are identical to or greater than the input image, according to the outputResizing parameter. | Image | nullptr | |||||
| Parameter Name | Description | Type | Supported Values | Default Value | |||||
|---|---|---|---|---|---|---|---|---|---|
|
input_image |
The input image. | image | Binary, Label, Grayscale or Multispectral | None | ||||
|
rotation_angle |
The angle of the rotation in degrees. | float64 | Any value | 90 | ||||
|
center_mode |
The way to define the rotation center
|
enumeration | IMAGE_CENTER | |||||
|
rotation_center |
The rotation center coordinates. This parameter is ignored in IMAGE_CENTER mode. | vector2d | Any value | [0, 0] | ||||
|
interpolation_type |
The interpolation mode. Method used to calculate the intensity of each pixel in the result image.
|
enumeration | NEAREST_NEIGHBOR | |||||
|
output_resizing |
Resize the output image to make all input data visible in the output image if set to True. Preserve the input dimension if set to False. | bool | True | |||||
|
padding_value |
The background value for pixels with no correpondant point in the input image. | float64 | Any value | 0 | ||||
|
output_image |
The output image. Its type is forced to the same values as the input. Its dimensions are identical to or greater than the input image, according to the outputResizing parameter. | image | None | |||||
| Parameter Name | Description | Type | Supported Values | Default Value | |||||
|---|---|---|---|---|---|---|---|---|---|
|
inputImage |
The input image. | Image | Binary, Label, Grayscale or Multispectral | null | ||||
|
rotationAngle |
The angle of the rotation in degrees. | Float64 | Any value | 90 | ||||
|
centerMode |
The way to define the rotation center
|
Enumeration | IMAGE_CENTER | |||||
|
rotationCenter |
The rotation center coordinates. This parameter is ignored in IMAGE_CENTER mode. | Vector2d | Any value | {0f, 0f} | ||||
|
interpolationType |
The interpolation mode. Method used to calculate the intensity of each pixel in the result image.
|
Enumeration | NEAREST_NEIGHBOR | |||||
|
outputResizing |
Resize the output image to make all input data visible in the output image if set to True. Preserve the input dimension if set to False. | Bool | true | |||||
|
paddingValue |
The background value for pixels with no correpondant point in the input image. | Float64 | Any value | 0 | ||||
|
outputImage |
The output image. Its type is forced to the same values as the input. Its dimensions are identical to or greater than the input image, according to the outputResizing parameter. | Image | null | |||||
Object Examples
auto polystyrene = ioformat::readImage( std::string( IMAGEDEVDATA_IMAGES_FOLDER ) + "polystyrene.tif" );
Rotate2d rotate2dAlgo;
rotate2dAlgo.setInputImage( polystyrene );
rotate2dAlgo.setRotationAngle( 40.5 );
rotate2dAlgo.setCenterMode( Rotate2d::CenterMode::IMAGE_CENTER );
rotate2dAlgo.setRotationCenter( {15.5, 32} );
rotate2dAlgo.setInterpolationType( Rotate2d::InterpolationType::NEAREST_NEIGHBOR );
rotate2dAlgo.setOutputResizing( true );
rotate2dAlgo.setPaddingValue( 0 );
rotate2dAlgo.execute();
std::cout << "outputImage:" << rotate2dAlgo.outputImage()->toString();
polystyrene = ioformat.read_image(imagedev_data.get_image_path("polystyrene.tif"))
rotate_2d_algo = imagedev.Rotate2d()
rotate_2d_algo.input_image = polystyrene
rotate_2d_algo.rotation_angle = 40.5
rotate_2d_algo.center_mode = imagedev.Rotate2d.IMAGE_CENTER
rotate_2d_algo.rotation_center = [15.5, 32]
rotate_2d_algo.interpolation_type = imagedev.Rotate2d.NEAREST_NEIGHBOR
rotate_2d_algo.output_resizing = True
rotate_2d_algo.padding_value = 0
rotate_2d_algo.execute()
print("output_image:", str(rotate_2d_algo.output_image))
ImageView polystyrene = ViewIO.ReadImage( @"Data/images/polystyrene.tif" );
Rotate2d rotate2dAlgo = new Rotate2d
{
inputImage = polystyrene,
rotationAngle = 40.5,
centerMode = Rotate2d.CenterMode.IMAGE_CENTER,
rotationCenter = new double[]{15.5, 32},
interpolationType = Rotate2d.InterpolationType.NEAREST_NEIGHBOR,
outputResizing = true,
paddingValue = 0
};
rotate2dAlgo.Execute();
Console.WriteLine( "outputImage:" + rotate2dAlgo.outputImage.ToString() );
Function Examples
auto polystyrene = ioformat::readImage( std::string( IMAGEDEVDATA_IMAGES_FOLDER ) + "polystyrene.tif" );
auto result = rotate2d( polystyrene, 40.5, Rotate2d::CenterMode::IMAGE_CENTER, {15.5, 32}, Rotate2d::InterpolationType::NEAREST_NEIGHBOR, true, 0 );
std::cout << "outputImage:" << result->toString();
polystyrene = ioformat.read_image(imagedev_data.get_image_path("polystyrene.tif"))
result = imagedev.rotate_2d(polystyrene, 40.5, imagedev.Rotate2d.IMAGE_CENTER, [15.5, 32], imagedev.Rotate2d.NEAREST_NEIGHBOR, True, 0)
print("output_image:", str(result))
ImageView polystyrene = ViewIO.ReadImage( @"Data/images/polystyrene.tif" );
IOLink.ImageView result = Processing.Rotate2d( polystyrene, 40.5, Rotate2d.CenterMode.IMAGE_CENTER, new double[]{15.5, 32}, Rotate2d.InterpolationType.NEAREST_NEIGHBOR, true, 0 );
Console.WriteLine( "outputImage:" + result.ToString() );