Pattern Recognition
This group provides a package of pattern recognition functions based on standard correlations.
- BinaryCorrelation2d: Performs a logical correlation between a binary two-dimensional image and a binary kernel.
- CrossCorrelation2d: Performs a correlation by convolution between a two-dimensional grayscale image and a grayscale kernel.
- CorrelationByDifference2d: Performs a correlation by the difference between a two-dimensional grayscale image and a grayscale kernel.
- CorrelationBySignChange2d: Performs a correlation by sign change between a two-dimensional grayscale image and a grayscale kernel.
Some tools facilitating the exploitation of correlation results can be found in the
Image Statistics section.
CrossCorrelation2d, CorrelationByDifference2d or CorrelationBySignChange2d can be used for grayscale image correlation and BinaryCorrelation2d for binary image correlation.
The grayscale correlation algorithms propose local luminosity and/or contrast normalization adjustments. There are 4 different correlation types (see CorrelationMode parameter):
The actual calculation depends on the image type:
Correlation algorithms provide a step parameter (OffsetMode parameter, except for CrossCorrelation2d). which speeds up the operation by calculating 1 value out of each step, as shown in Figure 1.
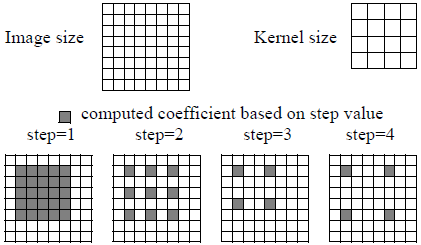
Figure 1. Standard Correlation
All uncomputed values (white pixels in Figure 1) are set to $-1 \times 10^{10}$ in the output image.
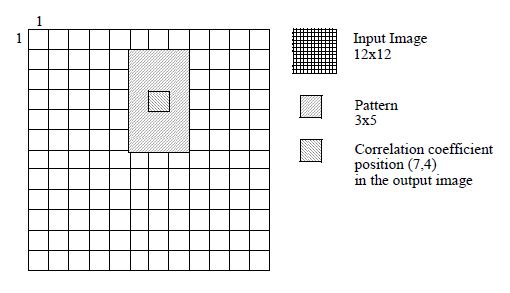
Figure 2. Correlation coefficient for odd dimensions
If the pattern dimensions are even, the position of the correlation coefficient is the closest pixel position to the top and the left.
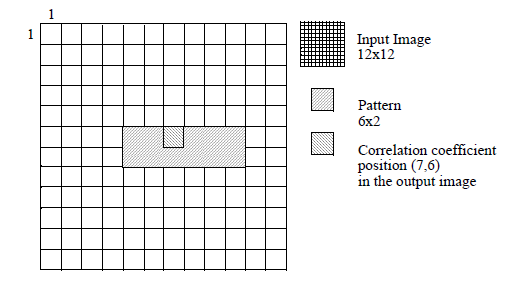
Figure 3. Correlation coefficient for even dimensions
These algorithms also return an output object CorrelationMsr which contains:
Image Correlation
The correlation filters allow the detection of rectangular pattern inside an input image in accordance with a matching criterion.CrossCorrelation2d, CorrelationByDifference2d or CorrelationBySignChange2d can be used for grayscale image correlation and BinaryCorrelation2d for binary image correlation.
The grayscale correlation algorithms propose local luminosity and/or contrast normalization adjustments. There are 4 different correlation types (see CorrelationMode parameter):
- DIRECT: Direct correlation (no normalization).
- MEAN: Mean normalized correlation (luminosity).
- VARIANCE: Variance normalized correlation (contrast).
- MEAN_VARIANCE: Mean and variance normalized correlation (luminosity and contrast).
The actual calculation depends on the image type:
- logical for BinaryCorrelation2d,
- multiplication for CrossCorrelation2d,
- difference CorrelationByDifference2d or
- sign change criterion CorrelationBySignChange2d.
Correlation algorithms provide a step parameter (OffsetMode parameter, except for CrossCorrelation2d). which speeds up the operation by calculating 1 value out of each step, as shown in Figure 1.

Figure 1. Standard Correlation
All uncomputed values (white pixels in Figure 1) are set to $-1 \times 10^{10}$ in the output image.
Luminosity and Contrast normalization
The luminosity and contrast normalization is controlled by one of the 4 correlation types:- DIRECT: Direct correlation (no normalization). $$ S(P, K) $$
- MEAN: Mean normalized correlation (luminosity). $$ S(P-\mu(P), K-\mu(K)) $$
- VARIANCE: Variance normalized correlation (contrast). $$ S\left (\frac{P}{\sqrt{\sigma^2(P)}}, \frac{K}{\sqrt{\sigma^2(K)}}\right ) $$
- MEAN_VARIANCE: Mean and variance normalized correlation (luminosity and contrast). $$ S\left (\frac{P-\mu(P)}{\sqrt{\sigma^2(P)}}, \frac{K-\mu(K)}{\sqrt{\sigma^2(K)}}\right ) $$
Output Image Normalization
During the correlation the minimum and the maximum values are calculated $(min, max)$. At the end of the filtering process, the correlation image is normalized between -1 and 1. The normalization depends on the following algorithm: $$ \Delta = \frac{max-min}{2} $$ $$ \mu = \frac{max+min}{2} $$ $$ \begin{array}{ll} O'(i, j) = \frac{O(i, j)-\mu}{\Delta} & \mbox{by default} \\ O'(i, j) = -1 \times \frac{O(i, j)-\mu}{\Delta} & \mbox{for correlation by difference} \end{array} $$ where $O'$ is the normalized image of the correlation image $O$.Position of the Correlation Coefficients
If the pattern dimensions are odd, the position of the correlation coefficient is centered in the pattern and corresponds to a pixel position.
Figure 2. Correlation coefficient for odd dimensions
If the pattern dimensions are even, the position of the correlation coefficient is the closest pixel position to the top and the left.

Figure 3. Correlation coefficient for even dimensions
Output Data
The correlation filters return a floating point correlation image. At the end of the process, this correlation image is converted between -1 and 1 (worst and best matching detected). The non-calculated points are set to -1E10.These algorithms also return an output object CorrelationMsr which contains:
- The position of the best matching ( matchingPositionX, matchingPositionY),
- The minimum and the maximum values of the correlation image before the conversion (minComputed, maxComputed),
- The theoretical minimum and maximum correlation values before the conversion ( minTheoretical, maxTheoretical).
© 2025 Thermo Fisher Scientific Inc. All rights reserved.