Geodesic Transformations
Algorithms based on geodesic propagations such as reconstructions.
- ReconstructionFromMarkers2d: Rebuilds a binary image starting from markers.
- ReconstructionFromMarkers3d: ReconstructionFromMarkers3d rebuilds a binary image starting from markers.
- GrayscaleReconstruction2d: Performs a two-dimensional numerical reconstruction, starting from a grayscale marker image, into a grayscale input image.
- GrayscaleReconstruction3d: Performs a three-dimensional numerical reconstruction, starting from a grayscale marker image, into a grayscale input image.
- GrayscaleFillHoles2d: Fills holes in particles of a two-dimensional grayscale image.
- GrayscaleFillHoles3d: Fills holes in particles of a three-dimensional grayscale image.
- HExtrema2d: Detects and merges the local maxima or minima of a two-dimensional grayscale image and marks them in a binary image.
- HExtrema3d: Detects and merges the local maxima or minima of a three-dimensional grayscale image and marks them in a binary image.
- RegionalExtrema2d: Computes the regional maxima or minima of a two-dimensional grayscale image and marks them in a binary image.
- RegionalExtrema3d: Computes the regional maxima or minima of a three-dimensional grayscale image and marks them in a binary image.
- UltimateErosion: Computes the ultimate eroded set of a binary image.
Definition of Geodesy
Geodesy is by definition the science of measuring the shape of the earth. When applied to image processing, it is the science of measuring the exact shape of objects included in an image.The geodesic distance is defined as follows:
- If two points $x$ and $y$ belong to $X$, then $d_X(x,y)$ is the shortest distance between the two points with the condition that the entire path between the points is included in the particle $X$.
- If one of the points is outside, then $d_X(x,z) = \infty$.
- If the points belong to 2 disjointed components, then $d_X(x,y) = \infty$
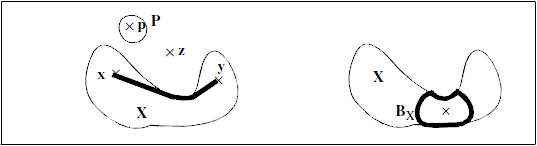
Figure 1. Geodesic measurement
The geodesic notion implies that each particle is fully independent of its neighbours in the image. Moreover, one may introduce the geodesic erosion and dilation.
The geodesic dilation is equivalent to a reconstruction in the continuous space. One can show that a discrete geodesic dilation of size $N$ is actually $N$ dilations of size 1, each dilation being followed by an intersection with the set $X$. In this case, the underlying discrete distance is defined by the structuring element.
The propagation function is then defined as: $$ t_X(x) = Sup\{d_X(x,y), y \in X\} $$ It corresponds to the geodesic distance between the point $x$ and the furthest point of $X$.
© 2025 Thermo Fisher Scientific Inc. All rights reserved.