Erosion And Dilation
Morphological erosion and dilation algorithms.
- Erosion2d: Performs a two-dimensional erosion using a structuring element matching with a square or a cross.
- Erosion3d: Performs a three-dimensional erosion using a structuring element matching with a full or partial cube.
- Dilation2d: Performs a two-dimensional dilation using a structuring element matching with a square or a cross.
- Dilation3d: Performs a three-dimensional dilation using a structuring element matching with a full or partial cube.
- ErosionDisk2d: Performs a two-dimensional erosion using a structuring element matching with a disk.
- ErosionDisk3d: Performs a three-dimensional erosion using a structuring element matching with an oriented disk.
- ErosionBall3d: Performs a three-dimensional erosion using a structuring element matching with a sphere.
- DilationDisk2d: Performs a two-dimensional dilation using a structuring element matching with a disk.
- DilationDisk3d: Performs a three-dimensional dilation using a structuring element matching with an oriented disk.
- DilationBall3d: Performs a three-dimensional erosion using a structuring element matching with a sphere.
- ErosionLine2d: Performs a two-dimensional erosion using a structuring element matching with a line.
- ErosionLine3d: Performs a three-dimensional erosion using a structuring element matching with a line.
- DilationLine2d: Performs a two-dimensional dilation using a structuring element matching with a line.
- DilationLine3d: Performs a three-dimensional dilation using a structuring element matching with a line.
- ErosionColor2d: Performs an erosion on a true-color image using a structuring element matching with a square.
- DilationColor2d: Performs a dilation on a true-color image using a structuring element matching with a square.
- SelectiveErosion2d: Erodes objects of a two-dimensional binary image conditionally to a local constraint.
- SelectiveErosion3d: Erodes objects of a three-dimensional binary image conditionally to a local constraint.
- SelectiveDilation2d: Dilates objects of a two-dimensional binary image conditionally to a local constraint.
- SelectiveDilation3d: Dilates objects of a three-dimensional binary image conditionally to a local constraint.
For an introduction: section Mathematical Morphology.
Erosion operations are reiterative: repeating an erosion or dilation of size 1 N times has the same effect as performing a single erosion with a structuring element of size N.
In Figure 1 the binary image is $I$, and $X$ denotes the set of points with a value of 1. The erosion of $I$ by the structuring element $B$ results in the set of points $x$, where the disk representing $B$ and centered on $x$ is totally included in the set of points $X$. The erosion of $I$ can be denoted as $E_B(I)$ or $E(I)$.

Figure 1. Erosion applied to a binary image
The eroded set of $X$ by the structuring element $B$ is: $E(X)=\left\{ x ~; ~ B_x \subset X \right\}$
It may also be written as: $E(X)=X \ominus B$
The value of the structuring element $B$ varies depending on the type of erosion.
On a gray level image, the erosion by the structuring element $B$ is the search for the minimal value of intensities within $B$.
Dilation operations are reiterative: repeating a dilation of size 1 N times has the same effect as performing a single dilation with a structuring element of size N.
In Figure 2, the binary image is $I$, and $X$ denotes the set of points with a value of 1. The dilation of $I$ by the structuring element $B$ results in the set of points $x$, where the disk representing $B$ and centered on $x$ has a non-empty intersection with the set of points $X$. The dilation of $I$ can be denoted as $D_B(I)$ or $D(I)$.
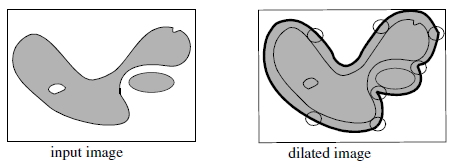
Figure 2. Dilation applied to a binary image
The dilated set of X by the structuring element B is: $D(X)=\left\{ x ~; ~ B_x \cap X \neq \varnothing \right\}$
It may also be expressed as: $D(X)=X \oplus B$
The value of the structuring element $B$ varies depending on the type of dilation.
On a gray level image, the dilation by the structuring element B is the search for the maximum value of intensities within $B$:
Introduction to Erosion
In an erosion, pixel values within the structuring element are set to the minimum value of the element. In a binary image, an erosion removes isolated points and small particles, shrinks other particles, discards peaks at the object boundaries, and disconnects some particles.Erosion operations are reiterative: repeating an erosion or dilation of size 1 N times has the same effect as performing a single erosion with a structuring element of size N.
In Figure 1 the binary image is $I$, and $X$ denotes the set of points with a value of 1. The erosion of $I$ by the structuring element $B$ results in the set of points $x$, where the disk representing $B$ and centered on $x$ is totally included in the set of points $X$. The erosion of $I$ can be denoted as $E_B(I)$ or $E(I)$.

Figure 1. Erosion applied to a binary image
The eroded set of $X$ by the structuring element $B$ is: $E(X)=\left\{ x ~; ~ B_x \subset X \right\}$
It may also be written as: $E(X)=X \ominus B$
The value of the structuring element $B$ varies depending on the type of erosion.
On a gray level image, the erosion by the structuring element $B$ is the search for the minimal value of intensities within $B$.
- 2D image : $E\left\{I(x,y)\right\}=Min\left\{I(x_i,y_j);(x_i,y_j) ~ \in B \right\}$.
- 3D image : $E\left\{I(x,y,z)\right\}=Min\left\{I(x_i,y_j,z_k);(x_i,y_j,z_k) ~ \in B \right\}$.
Introduction to Dilation
A dilation is the opposite of an erosion. In a dilation, pixel values within the structuring element are set to the maximum value of the pixel neighborhood. In a binary image, a dilation fills the small holes inside particles and gulfs at the object boundaries, enlarges the size of the particles, and may connect neighboring particles.Dilation operations are reiterative: repeating a dilation of size 1 N times has the same effect as performing a single dilation with a structuring element of size N.
In Figure 2, the binary image is $I$, and $X$ denotes the set of points with a value of 1. The dilation of $I$ by the structuring element $B$ results in the set of points $x$, where the disk representing $B$ and centered on $x$ has a non-empty intersection with the set of points $X$. The dilation of $I$ can be denoted as $D_B(I)$ or $D(I)$.

Figure 2. Dilation applied to a binary image
The dilated set of X by the structuring element B is: $D(X)=\left\{ x ~; ~ B_x \cap X \neq \varnothing \right\}$
It may also be expressed as: $D(X)=X \oplus B$
The value of the structuring element $B$ varies depending on the type of dilation.
On a gray level image, the dilation by the structuring element B is the search for the maximum value of intensities within $B$:
- 2D image : $D\left\{I(x,y)\right\}=Max\left\{I(x_i,y_j);(x_i,y_j) ~ \in B \right\}$.
- 3D image : $D\left\{I(x,y,z)\right\}=Max\left\{I(x_i,y_j,z_k);(x_i,y_j,z_k) ~ \in B \right\}$.