DobFilter2d
Appproximates a Laplacian as the difference of two box filters applied on the same two-dimensional image.
Access to parameter description
For an introduction:
The size of the kernels must be an odd number.
This operation applied to a 1D step edge is shown in Figure 1.
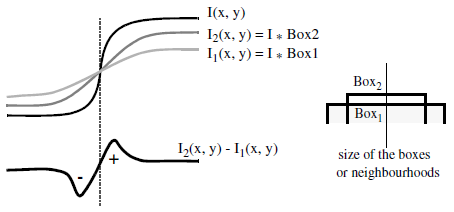
Figure 1. DOB approximation
DobFilter2d does not compute the Laplacian of an image, but is a good approximation and has the main advantage of not generating isolated points.
Typical ratios of the neighborhood sizes (width of Box1 / width of Box2) has a range between 1.5 and 2.5. Box1 and Box2 are respectively parametrized by the parameters largeBoxSize and smallBoxSize.
For example, kernels of size 5x5/3x3 or 9x9/5x5 can be used.
To keep a correct representation of the edges and a maximum of detail, using too large a kernel is not recommended (3, 5 and 7 are the most frequent values).
The deviation between the two masks has a direct effect on the edges. If the difference is too large, the edges are very thick and all small details disappear. If the difference is small (less than 4), the edges are very thin and details more precise.
See also
Access to parameter description
For an introduction:
- section Edge Detection
- section Laplacian
- section Images Filters
The size of the kernels must be an odd number.
This operation applied to a 1D step edge is shown in Figure 1.
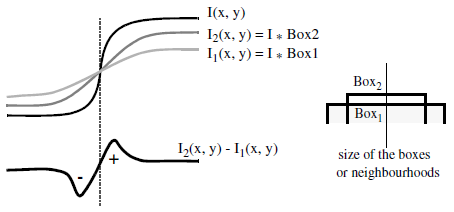
Figure 1. DOB approximation
DobFilter2d does not compute the Laplacian of an image, but is a good approximation and has the main advantage of not generating isolated points.
Typical ratios of the neighborhood sizes (width of Box1 / width of Box2) has a range between 1.5 and 2.5. Box1 and Box2 are respectively parametrized by the parameters largeBoxSize and smallBoxSize.
For example, kernels of size 5x5/3x3 or 9x9/5x5 can be used.
To keep a correct representation of the edges and a maximum of detail, using too large a kernel is not recommended (3, 5 and 7 are the most frequent values).
The deviation between the two masks has a direct effect on the edges. If the difference is too large, the edges are very thick and all small details disappear. If the difference is small (less than 4), the edges are very thin and details more precise.
See also
Function Syntax
This function returns outputImage.
// Function prototype
std::shared_ptr< iolink::ImageView > dobFilter2d( std::shared_ptr< iolink::ImageView > inputImage, int32_t smallBoxSize, int32_t largeBoxSize, std::shared_ptr< iolink::ImageView > outputImage = NULL );
This function returns outputImage.
// Function prototype.
dob_filter_2d( input_image,
small_box_size = 3,
large_box_size = 7,
output_image = None )
This function returns outputImage.
// Function prototype.
public static IOLink.ImageView
DobFilter2d( IOLink.ImageView inputImage,
Int32 smallBoxSize = 3,
Int32 largeBoxSize = 7,
IOLink.ImageView outputImage = null );
Class Syntax
Parameters
| Parameter Name | Description | Type | Supported Values | Default Value | |
|---|---|---|---|---|---|
 |
inputImage |
The input image. | Image | Binary, Label, Grayscale or Multispectral | nullptr |
 |
smallBoxSize |
The size of the small box. | Int32 | >=1 | 3 |
 |
largeBoxSize |
The size of the large box. | Int32 | >=1 | 7 |
 |
outputImage |
The output image. | Image | nullptr | |
| Parameter Name | Description | Type | Supported Values | Default Value | |
|---|---|---|---|---|---|
 |
input_image |
The input image. | image | Binary, Label, Grayscale or Multispectral | None |
 |
small_box_size |
The size of the small box. | int32 | >=1 | 3 |
 |
large_box_size |
The size of the large box. | int32 | >=1 | 7 |
 |
output_image |
The output image. | image | None | |
| Parameter Name | Description | Type | Supported Values | Default Value | |
|---|---|---|---|---|---|
 |
inputImage |
The input image. | Image | Binary, Label, Grayscale or Multispectral | null |
 |
smallBoxSize |
The size of the small box. | Int32 | >=1 | 3 |
 |
largeBoxSize |
The size of the large box. | Int32 | >=1 | 7 |
 |
outputImage |
The output image. | Image | null | |
Object Examples
std::shared_ptr< iolink::ImageView > polystyrene = ioformat::readImage( std::string( IMAGEDEVDATA_IMAGES_FOLDER ) + "polystyrene.tif" ); DobFilter2d dobFilter2dAlgo; dobFilter2dAlgo.setInputImage( polystyrene ); dobFilter2dAlgo.setSmallBoxSize( 3 ); dobFilter2dAlgo.setLargeBoxSize( 7 ); dobFilter2dAlgo.execute(); std::cout << "outputImage:" << dobFilter2dAlgo.outputImage()->toString();
polystyrene = ioformat.read_image(imagedev_data.get_image_path("polystyrene.tif"))
dob_filter_2d_algo = imagedev.DobFilter2d()
dob_filter_2d_algo.input_image = polystyrene
dob_filter_2d_algo.small_box_size = 3
dob_filter_2d_algo.large_box_size = 7
dob_filter_2d_algo.execute()
print( "output_image:", str( dob_filter_2d_algo.output_image ) )
ImageView polystyrene = ViewIO.ReadImage( @"Data/images/polystyrene.tif" );
DobFilter2d dobFilter2dAlgo = new DobFilter2d
{
inputImage = polystyrene,
smallBoxSize = 3,
largeBoxSize = 7
};
dobFilter2dAlgo.Execute();
Console.WriteLine( "outputImage:" + dobFilter2dAlgo.outputImage.ToString() );
Function Examples
std::shared_ptr< iolink::ImageView > polystyrene = ioformat::readImage( std::string( IMAGEDEVDATA_IMAGES_FOLDER ) + "polystyrene.tif" ); auto result = dobFilter2d( polystyrene, 3, 7 ); std::cout << "outputImage:" << result->toString();
polystyrene = ioformat.read_image(imagedev_data.get_image_path("polystyrene.tif"))
result = imagedev.dob_filter_2d( polystyrene, 3, 7 )
print( "output_image:", str( result ) )
ImageView polystyrene = ViewIO.ReadImage( @"Data/images/polystyrene.tif" ); IOLink.ImageView result = Processing.DobFilter2d( polystyrene, 3, 7 ); Console.WriteLine( "outputImage:" + result.ToString() );