Image Filtering
This category gathers filtering algorithms (for example, for denoising an image or enhancing its contrast).
- Grayscale Transforms: This group contains operations dedicated to enhance grayscale images.
- Color Transforms: This group contains algorithms dedicated to be applied on, or to produce, color images.
- Smoothing And Denoising: This group contains algorithms for removing noise from images.
- Sharpening: This group contains filters that enhance the edges of objects and adjust contrast and shading characteristics.
- Texture Filters: This group contains algorithms that reveal texture attributes.
- Frequency Domain: This group contains FFT's and related algorithms working in the frequency domain.
This category mainly contains algorithms that transform an image into
another image, generally of the same type.
A common problem in filtering theory is to estimate a signal mixed with noise.
A solution is the moving average , where the value of each pixel is replaced by the average of its neighbors (Figure 1). This is based on the assumption that short ranged variations result from noise. The filtered output can then be viewed as the main trend of the function.
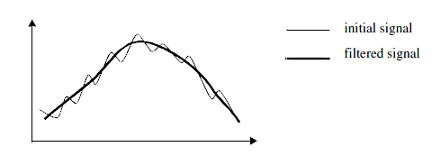
Figure 1. A moving average
Local changes in intensity present another common problem. Various filters can detect sharp transitions to enhance, contrast, or detect edges.
The Edge Detection algorithms use these types of filters.
Apart from the examples above, specific filters can be designed depending on the type of desired transition, such as:
If $f$ is an image $(f \in R^2)$, the output function is the filtered image.
Linear filters are widely used because they are easy to implement and, often, very intuitive.
A filter $\phi$ is linear if:
The non-linear filters in the Image Filtering category are shift invariant filters; for instance, filters such that: $\phi(f_h) = [\phi(f)]_h$ where $f_h$ denotes the function $f$ translated by vector $h$.
Shift invariant filters have the same effect on $f$ and its translated representations, which means that it is based on neighborhood operators where the same operations are performed around each pixel of the image.
Image Filters
A filter transforms an image to emphasize or stress a specific feature of its structure. Filtering techniques are often useful to extract desired information from input data or simply to improve the appearance of the input data. For example, filtering techniques are used to remove noise from corrupted images or to enhance poorly contrasted images.A common problem in filtering theory is to estimate a signal mixed with noise.
A solution is the moving average , where the value of each pixel is replaced by the average of its neighbors (Figure 1). This is based on the assumption that short ranged variations result from noise. The filtered output can then be viewed as the main trend of the function.

Figure 1. A moving average
Local changes in intensity present another common problem. Various filters can detect sharp transitions to enhance, contrast, or detect edges.
The Edge Detection algorithms use these types of filters.
Apart from the examples above, specific filters can be designed depending on the type of desired transition, such as:
- Removing a grid consisting of uniformly spaced dark lines superimposed on an image.
- Restoring an image blurred by some degradation processes. (A difficult problem, the solution to which requires a very good knowledge of the degradation process itself.)
If $f$ is an image $(f \in R^2)$, the output function is the filtered image.
Linear and Non-linear Filters
Filters are usually distinguished between linear and non-linear.Linear filters are widely used because they are easy to implement and, often, very intuitive.
A filter $\phi$ is linear if:
- $\phi(f + g) = \phi(f) + \phi(g)$
- $\phi(\lambda f) = \phi\lambda(f) \quad \lambda \in R$
The non-linear filters in the Image Filtering category are shift invariant filters; for instance, filters such that: $\phi(f_h) = [\phi(f)]_h$ where $f_h$ denotes the function $f$ translated by vector $h$.
Shift invariant filters have the same effect on $f$ and its translated representations, which means that it is based on neighborhood operators where the same operations are performed around each pixel of the image.