CorrelationBySignChange2d
Performs a correlation by sign change between a two-dimensional grayscale image and a grayscale kernel.
Access to parameter description
For an introduction: section Image Correlation.
This algorithm performs a correlation with a sign change metric between a gray level image $I$ and a gray level kernel $K$, returning the correlation image $O$.
$S$ is the sign change criterion performed on the difference image. It corresponds to the number of sign changes calculated on every line.
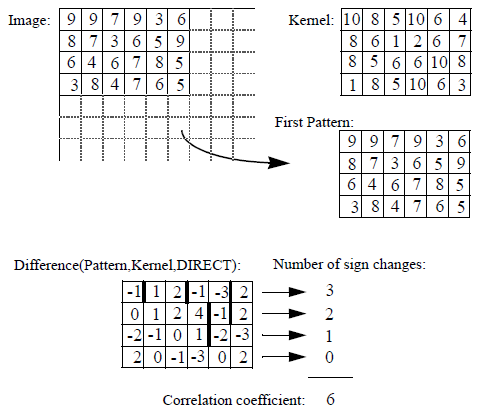
Figure 1. Example of sign correlation
The object in the model and the object in the image have luminosity, contrast, and noise differences. After normalization depending on the correlation type, the sign change criterion is applied on the difference image. The noise is supposed to be additive and zero mean. The statistical density function of the noise is supposed to be symmetrical. The best matching will correspond to the maximum number of sign changes.
This correlation gives very good results with big kernels. It was created for medical applications where images are often very noisy.
The different possibilities for selecting a correlation peak are presented below using a 1-D correlation between an image and kernel. In the image, the kernel appears 6 times with different contrast and luminosity.
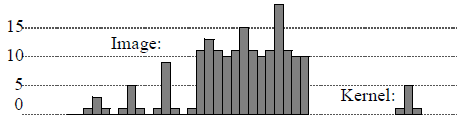
Figure 2. 1D image and kernel
The 6 examples show the kernel appearing with different contrast and luminosity.
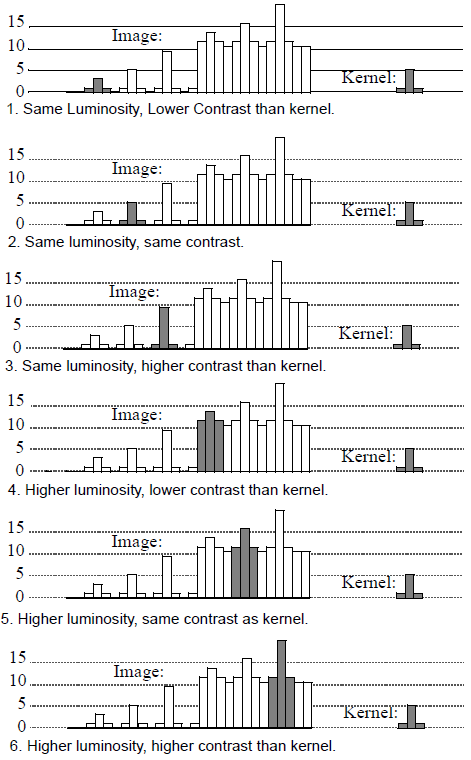
Figure 3. Examples of possible 1D correlation
The correlation by sign change metric is computed in accordance with the CorrelationMode parameter.
where: $$ \mu(K)=\frac{\sum\limits_{i=1}^{kx} \sum\limits_{j=1}^{ky} K(i,j)}{kx\times ky} $$ $$ \mu(I)(n,m)=\frac{\sum\limits_{i=1}^{kx} \sum\limits_{j=1}^{ky} I(n+i,m+j)}{kx\times ky} $$ $$ \sigma^2(K)=\sum_{i=1}^{kx} \sum_{j=1}^{ky} \left(K(i,j)-\mu(K)\right)^{2} $$ $$ \sigma^2(I)(n,m)=\sum_{i=1}^{kx} \sum_{j=1}^{ky} \left( I(n+i-\frac{kx}{2},m+j-\frac{ky}{2} ) - \mu(I)(n,m)\right)^{2} $$
Note: This algorithm returns the main correlation peak in the outputMeasurement object. More correlation peaks can be extracted from the outputImage correlation image with the LocalMaxima2d algorithm.
See also
Access to parameter description
For an introduction: section Image Correlation.
This algorithm performs a correlation with a sign change metric between a gray level image $I$ and a gray level kernel $K$, returning the correlation image $O$.
$S$ is the sign change criterion performed on the difference image. It corresponds to the number of sign changes calculated on every line.

Figure 1. Example of sign correlation
The object in the model and the object in the image have luminosity, contrast, and noise differences. After normalization depending on the correlation type, the sign change criterion is applied on the difference image. The noise is supposed to be additive and zero mean. The statistical density function of the noise is supposed to be symmetrical. The best matching will correspond to the maximum number of sign changes.
This correlation gives very good results with big kernels. It was created for medical applications where images are often very noisy.
The different possibilities for selecting a correlation peak are presented below using a 1-D correlation between an image and kernel. In the image, the kernel appears 6 times with different contrast and luminosity.

Figure 2. 1D image and kernel
The 6 examples show the kernel appearing with different contrast and luminosity.

Figure 3. Examples of possible 1D correlation
The correlation by sign change metric is computed in accordance with the CorrelationMode parameter.
DIRECT Correlation Mode
$$ O(n,m)=\sum_{i=1}^{kx} \sum_{j=1}^{ky} S\left[K(i,j)-I(n+i-\frac{kx}{2},m+j-\frac{ky}{2})\right] $$MEAN Correlation Mode
$$ O(n,m)=\sum_{i=1}^{kx} \sum_{j=1}^{ky} S\left[\left(K(i,j)-\mu(K)\right)-\left(I(n+i-\frac{kx}{2},m+j-; \frac{ky}{2})-\mu(I)(n,m)\right)\right] $$VARIANCE Correlation Mode
$$ O(n,m)=\frac{\sum\limits_{i=1}^{kx} \sum\limits_{j=1}^{ky} S\left[K(i,j)-I(n+i-\frac{kx}{2},m+j-; \frac{ky}{2})\right]}{\sqrt{\sigma^2(K)\times \sigma^2(I)(n,m)}} $$MEAN_VARIANCE Correlation Mode
$$ O(n,m)=\frac{\sum\limits_{i=1}^{kx} \sum\limits_{j=1}^{ky} S\left[\left(K(i,j)-\mu(K)\right)-; \left(I(n+i-\frac{kx}{2},m+j-\frac{ky}{2})-\mu(I)(n,m)\right)\right]}{\sqrt{\sigma^2(K)\times \sigma^2(I)(n,m)}} $$where: $$ \mu(K)=\frac{\sum\limits_{i=1}^{kx} \sum\limits_{j=1}^{ky} K(i,j)}{kx\times ky} $$ $$ \mu(I)(n,m)=\frac{\sum\limits_{i=1}^{kx} \sum\limits_{j=1}^{ky} I(n+i,m+j)}{kx\times ky} $$ $$ \sigma^2(K)=\sum_{i=1}^{kx} \sum_{j=1}^{ky} \left(K(i,j)-\mu(K)\right)^{2} $$ $$ \sigma^2(I)(n,m)=\sum_{i=1}^{kx} \sum_{j=1}^{ky} \left( I(n+i-\frac{kx}{2},m+j-\frac{ky}{2} ) - \mu(I)(n,m)\right)^{2} $$
Note: This algorithm returns the main correlation peak in the outputMeasurement object. More correlation peaks can be extracted from the outputImage correlation image with the LocalMaxima2d algorithm.
See also
Function Syntax
This function returns a CorrelationBySignChange2dOutput structure containing the outputImage and outputMeasurement output parameters.
// Output structure.
struct CorrelationBySignChange2dOutput
{
std::shared_ptr< iolink::ImageView > outputImage;
CorrelationMsr::Ptr outputMeasurement;
};
// Function prototype.
CorrelationBySignChange2dOutput
correlationBySignChange2d( std::shared_ptr< iolink::ImageView > inputImage,
std::shared_ptr< iolink::ImageView > inputKernelImage,
CorrelationBySignChange2d::OffsetMode offsetMode,
CorrelationBySignChange2d::CorrelationMode correlationMode,
std::shared_ptr< iolink::ImageView > outputImage = NULL,
CorrelationMsr::Ptr outputMeasurement = NULL );
This function returns a tuple containing the output_image and output_measurement output parameters.
// Function prototype.
correlation_by_sign_change_2d( input_image,
input_kernel_image,
offset_mode = CorrelationBySignChange2d.OffsetMode.OFFSET_1,
correlation_mode = CorrelationBySignChange2d.CorrelationMode.DIRECT,
output_image = None,
output_measurement = None )
This function returns a CorrelationBySignChange2dOutput structure containing the outputImage and outputMeasurement output parameters.
/// Output structure of the CorrelationBySignChange2d function.
public struct CorrelationBySignChange2dOutput
{
public IOLink.ImageView outputImage;
public CorrelationMsr outputMeasurement;
};
// Function prototype.
public static CorrelationBySignChange2dOutput
CorrelationBySignChange2d( IOLink.ImageView inputImage,
IOLink.ImageView inputKernelImage,
CorrelationBySignChange2d.OffsetMode offsetMode = ImageDev.CorrelationBySignChange2d.OffsetMode.OFFSET_1,
CorrelationBySignChange2d.CorrelationMode correlationMode = ImageDev.CorrelationBySignChange2d.CorrelationMode.DIRECT,
IOLink.ImageView outputImage = null,
CorrelationMsr outputMeasurement = null );
Class Syntax
Parameters
| Class Name | CorrelationBySignChange2d |
|---|
| Parameter Name | Description | Type | Supported Values | Default Value | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 |
inputImage |
The input grayscale image. | Image | Binary, Label or Grayscale | nullptr | ||||||||
 |
inputKernelImage |
The correlation kernel. | Image | Binary, Label or Grayscale | nullptr | ||||||||
 |
offsetMode |
The calculation offset, in pixels. The greater this value, computation is faster but detection is less precise.
|
Enumeration | OFFSET_1 | |||||||||
 |
correlationMode |
The normalization mode for correlation.
|
Enumeration | DIRECT | |||||||||
 |
outputImage |
The output correlation image. Its dimensions are forced to the same values as the input. Its data type is forced to floating point. | Image | nullptr | |||||||||
 |
outputMeasurement |
The correlation matching results. | CorrelationMsr | nullptr | |||||||||
Object Examples
std::shared_ptr< iolink::ImageView > polystyrene = ioformat::readImage( std::string( IMAGEDEVDATA_IMAGES_FOLDER ) + "polystyrene.tif" ); CorrelationBySignChange2d correlationBySignChange2dAlgo; correlationBySignChange2dAlgo.setInputImage( polystyrene ); correlationBySignChange2dAlgo.setInputKernelImage( polystyrene ); correlationBySignChange2dAlgo.setOffsetMode( CorrelationBySignChange2d::OffsetMode::OFFSET_1 ); correlationBySignChange2dAlgo.setCorrelationMode( CorrelationBySignChange2d::CorrelationMode::DIRECT ); correlationBySignChange2dAlgo.execute(); std::cout << "outputImage:" << correlationBySignChange2dAlgo.outputImage()->toString(); std::cout << "minComputed: " << correlationBySignChange2dAlgo.outputMeasurement()->minComputed( 0 ) ;
polystyrene = ioformat.read_image(imagedev_data.get_image_path("polystyrene.tif"))
correlation_by_sign_change_2d_algo = imagedev.CorrelationBySignChange2d()
correlation_by_sign_change_2d_algo.input_image = polystyrene
correlation_by_sign_change_2d_algo.input_kernel_image = polystyrene
correlation_by_sign_change_2d_algo.offset_mode = imagedev.CorrelationBySignChange2d.OFFSET_1
correlation_by_sign_change_2d_algo.correlation_mode = imagedev.CorrelationBySignChange2d.DIRECT
correlation_by_sign_change_2d_algo.execute()
print( "output_image:", str( correlation_by_sign_change_2d_algo.output_image ) )
print( "minComputed: ", str( correlation_by_sign_change_2d_algo.output_measurement.min_computed( 0 ) ) )
ImageView polystyrene = ViewIO.ReadImage( @"Data/images/polystyrene.tif" );
CorrelationBySignChange2d correlationBySignChange2dAlgo = new CorrelationBySignChange2d
{
inputImage = polystyrene,
inputKernelImage = polystyrene,
offsetMode = CorrelationBySignChange2d.OffsetMode.OFFSET_1,
correlationMode = CorrelationBySignChange2d.CorrelationMode.DIRECT
};
correlationBySignChange2dAlgo.Execute();
Console.WriteLine( "outputImage:" + correlationBySignChange2dAlgo.outputImage.ToString() );
Console.WriteLine( "minComputed: " + correlationBySignChange2dAlgo.outputMeasurement.minComputed( 0 ) );
Function Examples
std::shared_ptr< iolink::ImageView > polystyrene = ioformat::readImage( std::string( IMAGEDEVDATA_IMAGES_FOLDER ) + "polystyrene.tif" ); auto result = correlationBySignChange2d( polystyrene, polystyrene, CorrelationBySignChange2d::OffsetMode::OFFSET_1, CorrelationBySignChange2d::CorrelationMode::DIRECT ); std::cout << "outputImage:" << result.outputImage->toString(); std::cout << "minComputed: " << result.outputMeasurement->minComputed( 0 ) ;
polystyrene = ioformat.read_image(imagedev_data.get_image_path("polystyrene.tif"))
result_output_image, result_output_measurement = imagedev.correlation_by_sign_change_2d( polystyrene, polystyrene, imagedev.CorrelationBySignChange2d.OFFSET_1, imagedev.CorrelationBySignChange2d.DIRECT )
print( "output_image:", str( result_output_image ) )
print( "minComputed: ", str( result_output_measurement.min_computed( 0 ) ) )
ImageView polystyrene = ViewIO.ReadImage( @"Data/images/polystyrene.tif" ); Processing.CorrelationBySignChange2dOutput result = Processing.CorrelationBySignChange2d( polystyrene, polystyrene, CorrelationBySignChange2d.OffsetMode.OFFSET_1, CorrelationBySignChange2d.CorrelationMode.DIRECT ); Console.WriteLine( "outputImage:" + result.outputImage.ToString() ); Console.WriteLine( "minComputed: " + result.outputMeasurement.minComputed( 0 ) );