LocalMaxima2d
Extracts the local maxima of an image using a two-dimensional neighborhood analysis.
Access to parameter description
This algorithm considers $I(i,j)$ as a local maximum of $I$ if the two conditions below are verified
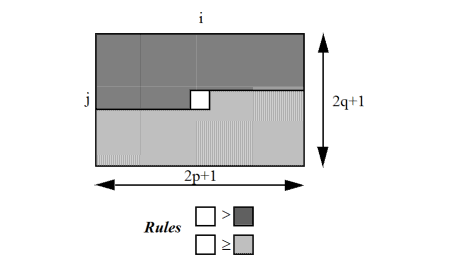
Figure 1. Graphic visualization of the 2D neighborhood analysis
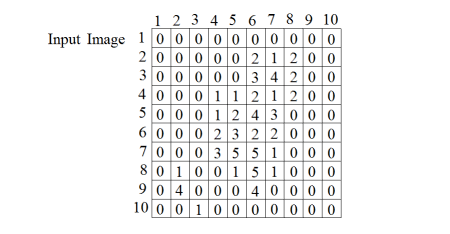
Figure 2. Input image for local maxima extraction

Figure 3. Extracted maxima with the first parameter set
The actual number of local maxima detected is 7.
The local maxima are located at positions: (7,3), (6,5), (5,7), (6,7), (6,8), (2,9) and (6,9)
This algorithm configuration corresponds to a single thresholding operator.

Figure 4. Extracted maxima with the second parameter set
The actual number of local maxima detected is 4.
The local maxima are located at positions: (7,3), (6,5), (5,7) and (2,9)
Note: If there is an area in the image at constant level, the algorithm returns the upper left corner of this area. The other points of this area are not considered as "local maxima".

Figure 5. Extracted maxima with the third parameter set
The actual number of local maxima detected is 2.
The local maxima are located at positions: (7,3) and (5,7)
Note: The algorithm is not performed on the image border depending on the $n$ and $m$ values. This is the reason why the point (2,9) is not considered as a local maximum.
On example 3, the algorithm detects 2 local maxima. The positions are converted to sub-pixel positions as follows
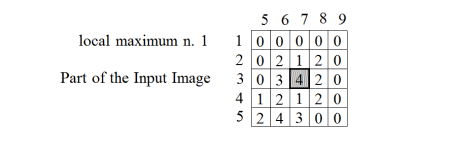
Figure 6. First maximum identified in example 3
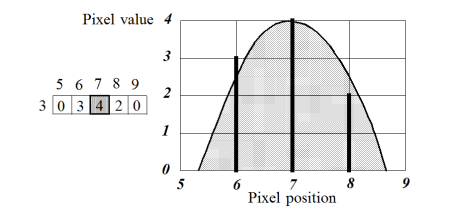
Figure 7. X sub-pixel position determined by parabola approximation
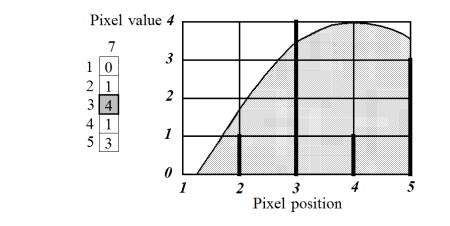
Figure 8. Y sub-pixel position determined by parabola approximation
The maximum detected in pixel precision at (7,3) becomes (6.95,4.05) with sub-pixel precision.
See also
Access to parameter description
This algorithm considers $I(i,j)$ as a local maximum of $I$ if the two conditions below are verified
-
1. $I(i,j)$ is a local maximum in a $(2p+1)\times(2q+1)$ neighborhood, i.e., considering $k \in [1,p]$,
$l \in [1,q]$ and m in [-p,p], $I(i,j)$
- $I(i,j)>I(i+m,j-l)$
- $I(i,j)>I(i-k,j)$
- $I(i,j) \geq I(i+k,j)$
- $I(i,j) \geq I(i+m,j+l)$
- $I(i,j)>threshold$

Figure 1. Graphic visualization of the 2D neighborhood analysis
Examples
The examples below show the effect of the LocalMaxima2d algorithm with different parameters sets applied on the image illustrated in Figure 2.
Figure 2. Input image for local maxima extraction
Example 1
First parameter set:- p=0
- q=0
- threshold=4
- number=50

Figure 3. Extracted maxima with the first parameter set
The actual number of local maxima detected is 7.
The local maxima are located at positions: (7,3), (6,5), (5,7), (6,7), (6,8), (2,9) and (6,9)
This algorithm configuration corresponds to a single thresholding operator.
Example 2
Second parameter set:- p=1
- q=1
- threshold=3
- number=50

Figure 4. Extracted maxima with the second parameter set
The actual number of local maxima detected is 4.
The local maxima are located at positions: (7,3), (6,5), (5,7) and (2,9)
Note: If there is an area in the image at constant level, the algorithm returns the upper left corner of this area. The other points of this area are not considered as "local maxima".
Example 3
Third parameter set:- p=2
- q=2
- threshold=3
- number=50

Figure 5. Extracted maxima with the third parameter set
The actual number of local maxima detected is 2.
The local maxima are located at positions: (7,3) and (5,7)
Note: The algorithm is not performed on the image border depending on the $n$ and $m$ values. This is the reason why the point (2,9) is not considered as a local maximum.
Sub-Pixel Position Determination
The maxima can be returned either as a discrete position in the image grid, or as a sub-pixel position by interpolation with parabola.On example 3, the algorithm detects 2 local maxima. The positions are converted to sub-pixel positions as follows

Figure 6. First maximum identified in example 3

Figure 7. X sub-pixel position determined by parabola approximation

Figure 8. Y sub-pixel position determined by parabola approximation
The maximum detected in pixel precision at (7,3) becomes (6.95,4.05) with sub-pixel precision.
See also
Function Syntax
This function returns outputMeasurement.
// Function prototype
LocalMaximaMsr::Ptr localMaxima2d( std::shared_ptr< iolink::ImageView > inputGrayImage, iolink::Vector2i32 localWindow, double thresholdRange, LocalMaxima2d::Precision precision, int32_t numberOfPatterns, LocalMaximaMsr::Ptr outputMeasurement = NULL );
This function returns outputMeasurement.
// Function prototype.
local_maxima_2d( input_gray_image,
local_window = [3, 3],
threshold_range = 0,
precision = LocalMaxima2d.Precision.PIXEL,
number_of_patterns = 1,
output_measurement = None )
This function returns outputMeasurement.
// Function prototype.
public static LocalMaximaMsr
LocalMaxima2d( IOLink.ImageView inputGrayImage,
int[] localWindow = null,
double thresholdRange = 0,
LocalMaxima2d.Precision precision = ImageDev.LocalMaxima2d.Precision.PIXEL,
Int32 numberOfPatterns = 1,
LocalMaximaMsr outputMeasurement = null );
Class Syntax
Parameters
| Class Name | LocalMaxima2d |
|---|
| Parameter Name | Description | Type | Supported Values | Default Value | |||||
|---|---|---|---|---|---|---|---|---|---|
 |
inputGrayImage |
The input grayscale image. | Image | Binary, Label or Grayscale | nullptr | ||||
 |
localWindow |
The neighborhood size in pixels, along the X and Y directions. | Vector2i32 | >0 | {3, 3} | ||||
 |
thresholdRange |
The threshold value higher than which maxima are retained. | Float64 | >=0 | 0 | ||||
 |
precision |
The precision of the maxima localization.
|
Enumeration | PIXEL | |||||
 |
numberOfPatterns |
The maximum number of patterns to be detected. | Int32 | >=1 | 1 | ||||
 |
outputMeasurement |
The result object containing the maxima positions. | LocalMaximaMsr | nullptr | |||||
Object Examples
std::shared_ptr< iolink::ImageView > polystyrene = ioformat::readImage( std::string( IMAGEDEVDATA_IMAGES_FOLDER ) + "polystyrene.tif" );
LocalMaxima2d localMaxima2dAlgo;
localMaxima2dAlgo.setInputGrayImage( polystyrene );
localMaxima2dAlgo.setLocalWindow( {3, 3} );
localMaxima2dAlgo.setThresholdRange( 0 );
localMaxima2dAlgo.setPrecision( LocalMaxima2d::Precision::PIXEL );
localMaxima2dAlgo.setNumberOfPatterns( 1 );
localMaxima2dAlgo.execute();
std::cout << "value: " << localMaxima2dAlgo.outputMeasurement()->value( ) ;
polystyrene = ioformat.read_image(imagedev_data.get_image_path("polystyrene.tif"))
local_maxima_2d_algo = imagedev.LocalMaxima2d()
local_maxima_2d_algo.input_gray_image = polystyrene
local_maxima_2d_algo.local_window = [3, 3]
local_maxima_2d_algo.threshold_range = 0
local_maxima_2d_algo.precision = imagedev.LocalMaxima2d.PIXEL
local_maxima_2d_algo.number_of_patterns = 1
local_maxima_2d_algo.execute()
print( "value: ", str( local_maxima_2d_algo.output_measurement.value( ) ) )
ImageView polystyrene = ViewIO.ReadImage( @"Data/images/polystyrene.tif" );
LocalMaxima2d localMaxima2dAlgo = new LocalMaxima2d
{
inputGrayImage = polystyrene,
localWindow = new int[]{3, 3},
thresholdRange = 0,
precision = LocalMaxima2d.Precision.PIXEL,
numberOfPatterns = 1
};
localMaxima2dAlgo.Execute();
Console.WriteLine( "value: " + localMaxima2dAlgo.outputMeasurement.value( ) );
Function Examples
std::shared_ptr< iolink::ImageView > polystyrene = ioformat::readImage( std::string( IMAGEDEVDATA_IMAGES_FOLDER ) + "polystyrene.tif" );
auto result = localMaxima2d( polystyrene, {3, 3}, 0, LocalMaxima2d::Precision::PIXEL, 1 );
std::cout << "value: " << result->value( ) ;
polystyrene = ioformat.read_image(imagedev_data.get_image_path("polystyrene.tif"))
result = imagedev.local_maxima_2d( polystyrene, [3, 3], 0, imagedev.LocalMaxima2d.PIXEL, 1 )
print( "value: ", str( result.value( ) ) )
ImageView polystyrene = ViewIO.ReadImage( @"Data/images/polystyrene.tif" );
LocalMaximaMsr result = Processing.LocalMaxima2d( polystyrene, new int[]{3, 3}, 0, LocalMaxima2d.Precision.PIXEL, 1 );
Console.WriteLine( "value: " + result.value( ) );