Geometric Transforms
This group contains transforms commonly used to align images.
- TranslateImage2d: Translates a two-dimensional image by a user-defined vector.
- TranslateImage3d: Translates a three-dimensional image by a user-defined vector.
- FlipImage2d: Flips a two-dimensional image along the X axis, Y axis, or the image center.
- FlipImage3d: Flips a three-dimensional image along the X, Y, or Z axis.
- TransposeImage2d: Swaps coordinates of a two-dimensional image.
- TransposeImage3d: Swaps coordinates of a three-dimensional image.
- SwapQuadrants: Performs a quadrant-wise translation in circular mode.
- Rotate2d: Applies a rotation of a given angle on a two-dimensional image around a given point or the center of the image.
- Rotate3d: Applies a rotation on a three-dimensional image around a user-defined point or the center of the image.
- RotateImage2d: Applies a rotation of a given angle and center on a two-dimensional image.
- RotateImage3d: Applies a rotation of a given angle on a three-dimensional image.
- RotateCenterImage2d: Applies a centered rotation of a given angle on a two-dimensional image.
- RotationGenerator3d: Computes a list of uniformly distributed three-dimensional rotations on the unit sphere.
- Resize2d: Generates a two-dimensional image with a new size using a user-defined interpolation mode.
- Resize3d: Generates a three-dimensional image with a new size using a user-defined interpolation mode.
- RescaleImage2d: Generates a two-dimensional image with a new size using a user-defined interpolation mode.
- RescaleImage3d: Generates a three-dimensional image with a new size using a user-defined interpolation mode.
- RescaleImageByFactor: Rescales the dimensions of a two-dimensional or three-dimensional image.
- ResampleAffine3d: Resamples an image by defining an oriented bounding box and a geometric transform.
- ResampleAffine2d: Resamples a two-dimensional image by defining an oriented bounding box and a geometric transform.
- ResampleElastic2d: Resamples an image after applying a transformation described by a displacement field.
- SurfaceUnfolding3d: Extracts a flattened 3D image from an input 3D image mapped to a surface mesh.
Geometric Transforms are usually used to align images. For example, if the subject and camera were not ideally
positioned, rotating the image may improve visualization.
Rotation and translation can be used to align successive sections of CT scans or confocal microscope images. A combination of geometric transformations is sometimes used to restore satellite or remote sensing images.
In addition, some image processing operations, such as erosion, dilation, and even edge detection, are usually implemented for the main directions of the grid: $0^\circ$, $45^\circ$, $90^\circ$, etc. To erode an image in the $20^\circ$ direction, you could first rotate the image $20^\circ$, and then perform a $0^\circ$ erosion. Be aware that the rotation distorts the image because of resampling.
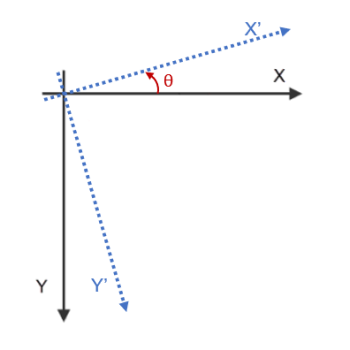
Figure 1. The angle corresponds to this convention for defining the orientation
The 3D Euler angle with ZXZ convention is a method of describing the orientation of a rigid body in three-dimensional space. It is defined by three consecutive rotations about the body's intrinsic axes, specifically the intial Z-axis $Z_1$, the new X-axis $X_2$, and the Z-axis produced by the two previous rotations $Z_3$, respectively.
The ZXZ convention is particularly useful for describing the orientation of objects with symmetrical shapes, such as spheres or cylinders.
To calculate the orientation of a rigid body using the ZXZ convention, the following steps can be followed:
The resulting orientation of the body can be represented by a 3x3 rotation matrix, which can be used to transform the coordinates of points in the body's coordinate system to the global coordinate system.
The rotation matrix for the ZXZ convention can be expressed as: $$R_{ZXZ}= R_{Z}(\alpha ).R_{X}(\beta ).R_{Z}(\gamma )$$ where $R_{Z}(\alpha )$, $R_{X}(\beta )$, and $R_{Z}(\gamma )$ represent the rotation matrices for the Z-axis, X-axis, and Z-axis rotations, respectively.
The individual rotation matrices can be defined as follows:
$$R_{Z}(\alpha)=\begin{pmatrix} cos(\alpha) & -sin(\alpha) & 0 \\ sin(\alpha) & cos(\alpha) & 0 \\ 0 & 0 & 1 \end{pmatrix}$$ $$R_{X}(\beta)=\begin{pmatrix} 1 & 0 & 0 \\ 0 & cos(\beta) & -sin(\beta) \\ 0 & sin(\beta) & cos(\beta) \end{pmatrix}$$ $$R_{Z}(\gamma)=\begin{pmatrix} cos(\gamma) & -sin(\gamma) & 0 \\ sin(\gamma) & cos(\gamma) & 0 \\ 0 & 0 & 1 \end{pmatrix}$$
It is important to note that the order of rotations matters in the ZXZ convention. The rotations are applied in the order of Z-axis, X-axis, and then Z-axis again.
Rotation and translation can be used to align successive sections of CT scans or confocal microscope images. A combination of geometric transformations is sometimes used to restore satellite or remote sensing images.
In addition, some image processing operations, such as erosion, dilation, and even edge detection, are usually implemented for the main directions of the grid: $0^\circ$, $45^\circ$, $90^\circ$, etc. To erode an image in the $20^\circ$ direction, you could first rotate the image $20^\circ$, and then perform a $0^\circ$ erosion. Be aware that the rotation distorts the image because of resampling.
Rotation conventions
The rotations are provided following a regular convention.2D rotations
In 2D, the rotation angle is given by a single value, considering the positive direction going from the Y-axis to the X-axis. Since ImageDev considers the origin of an image to be in its upper-left corner, the rotation visually occurs counterclockwise.
Figure 1. The angle corresponds to this convention for defining the orientation
3D rotations
In 3D, the rotations are given by Euler angles following the ZXZ convention with intrinsic rotations.The 3D Euler angle with ZXZ convention is a method of describing the orientation of a rigid body in three-dimensional space. It is defined by three consecutive rotations about the body's intrinsic axes, specifically the intial Z-axis $Z_1$, the new X-axis $X_2$, and the Z-axis produced by the two previous rotations $Z_3$, respectively.
The ZXZ convention is particularly useful for describing the orientation of objects with symmetrical shapes, such as spheres or cylinders.
To calculate the orientation of a rigid body using the ZXZ convention, the following steps can be followed:
- Rotate the body about $Z_1$ by an angle $\alpha$: This rotation is performed in the body's coordinate system.
- Rotate the body about $X_2$ by an angle $\beta$: This rotation is performed in the updated coordinate system after the first rotation.
- Rotate the body about $Z_3$ by an angle $\gamma$: This rotation is performed in the final coordinate system after the first two rotations.
The resulting orientation of the body can be represented by a 3x3 rotation matrix, which can be used to transform the coordinates of points in the body's coordinate system to the global coordinate system.
The rotation matrix for the ZXZ convention can be expressed as: $$R_{ZXZ}= R_{Z}(\alpha ).R_{X}(\beta ).R_{Z}(\gamma )$$ where $R_{Z}(\alpha )$, $R_{X}(\beta )$, and $R_{Z}(\gamma )$ represent the rotation matrices for the Z-axis, X-axis, and Z-axis rotations, respectively.
The individual rotation matrices can be defined as follows:
$$R_{Z}(\alpha)=\begin{pmatrix} cos(\alpha) & -sin(\alpha) & 0 \\ sin(\alpha) & cos(\alpha) & 0 \\ 0 & 0 & 1 \end{pmatrix}$$ $$R_{X}(\beta)=\begin{pmatrix} 1 & 0 & 0 \\ 0 & cos(\beta) & -sin(\beta) \\ 0 & sin(\beta) & cos(\beta) \end{pmatrix}$$ $$R_{Z}(\gamma)=\begin{pmatrix} cos(\gamma) & -sin(\gamma) & 0 \\ sin(\gamma) & cos(\gamma) & 0 \\ 0 & 0 & 1 \end{pmatrix}$$
It is important to note that the order of rotations matters in the ZXZ convention. The rotations are applied in the order of Z-axis, X-axis, and then Z-axis again.